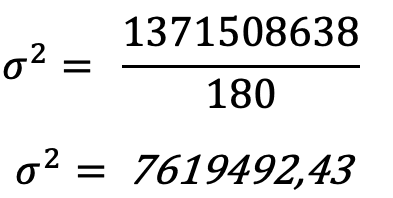De variantie is in de statistiek een maat voor de spreiding van een reeks waarden. Met andere woorden, het zegt iets over de mate waarin de waarden onderling verschillen. Hoe groter de variantie, hoe meer de afzonderlijke waarden onderling verschillen, en dus ook hoe meer de waarden van het “gemiddelde” afwijken. Binnen Lean Six Sigma komt de term variantie regelmatig voorbij. Daarom komen in deze blog alle ins en outs van variantie naar voren.
![]()
Waarom variantie?
Uit de inleiding wordt duidelijk: Hoe groter de variantie, hoe groter de spreiding of onderlinge verschillen zijn in een steekproef of populatie. De variantie berekenen we, omdat we door het berekenen van de variantie uiteindelijk de standaard deviatie kunnen berekenen. De standaard deviatie is een maat voor de spreiding van een variabele, verdeling of populatie. De standaarddeviatie is hierbij de wortel van de variantie.
De variantie en standaard deviatie zijn belangrijke gegevens voor het uitvoeren van diverse statistische tests. Wanneer een verdeling normaal verdeeld is, zijn het gemiddelde en de variantie (of standaardafwijking) de beste samenvattingsmaten.
Hoe bereken je de variantie?
Om de variantie te berekenen maken we gebruik van continue variabelen.
Voorbeeld berekenen van variantie
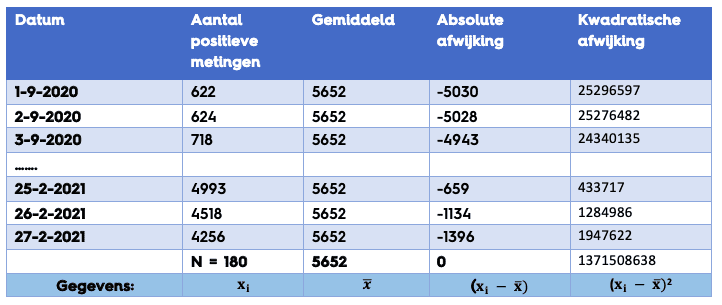
Stel dat we naar de variantie van het aantal coronabesmettingen gaan kijken in de periode van 1 september t/m 27 februari. We willen kijken of er veel variatie zit in het aantal besmettingen gedurende deze periode. We pakken in deze periode alle metingen per dag en gaan hier dus uit van een volledige populatie en niet van een steekproef.
Als we de variantie gaan berekenen krijgen we de volgende formule.
We zien in dit voorbeeld dat de variantie groot is. Als alle cijfers hetzelfde zouden zijn zou de variantie 0 zijn en er dus weinig variatie zitten in het aantal besmettingen.
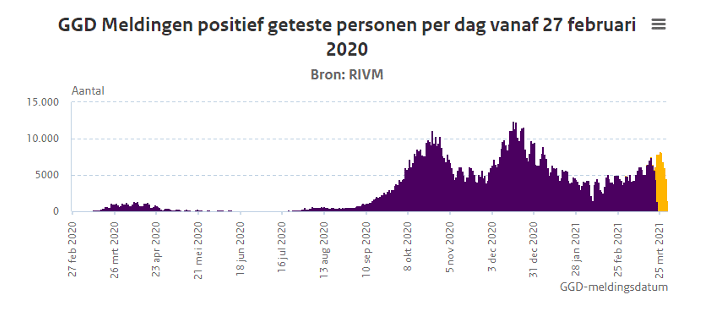
Hieronder in de grafiek kunnen we ook zien dat het aantal besmettingen in de periode van september tot februari ook flink variëren. En veel variatie is nooit een goed teken. Dat bekend dat een proces niet beheerst is en dus lastig te voorspellen.