In dit artikel gaan we je meer vertellen over de Gausskromme, oftewel de normale verdeling. Sommige studies bevatten veel statistiekvakken, denk bijvoorbeeld aan economische studies. P-waardes, percentielen en standaarddeviaties worden hierbij uitgebreid besproken, net als de normale verdeling. Maar wat als je deze achtergrond niet hebt en je toch wil verdiepen in Six Sigma? Na het lezen van dit artikel weet je precies wat er wordt bedoeld met een normale verdeling.
Voorbeeld van een normale verdeling
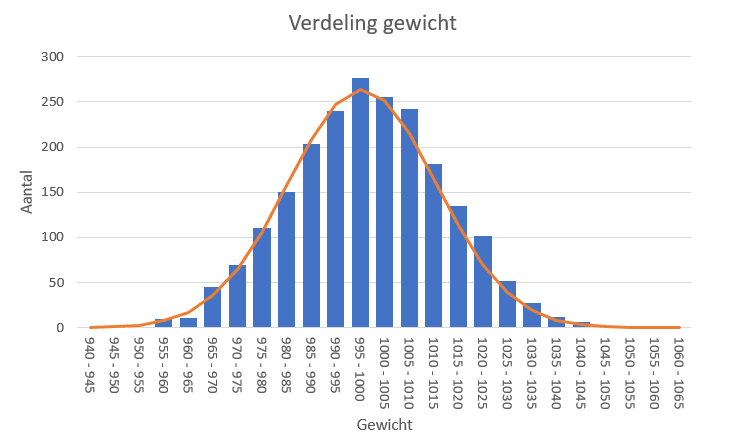
In de grafiek hieronder zie je de verdeling van het gewicht van 2000 zakken appels. Deze zak met appels koop je op de markt en weegt volgens de marktkoopman een kilo. In de werkelijkheid zal je zien dat niet iedere zak exact een kilo weegt, maar net iets meer of iets minder.
Wat is een normale verdeling?
Bij een groot aantal waarnemingen zie je een klokvorm in de grafiek komen, er is dan sprake van een normale verdeling. Op basis van het bovenstaande plaatje kunnen we daarom zeggen dat het gewicht van een zak appels naar alle waarschijnlijkheid is verdeeld volgens een normale verdeling. Hierbij is er een gemiddelde waarde μ (uit te spreken als ‘mu’) en wordt de mate van spreiding uitgedrukt in σ (uit te spreken als ‘sigma’). Deze twee waarden bepalen de exacte vorm van de grafiek.
Eigenschappen van een ideale normale verdeling
- Een normale verdeling is symmetrisch ten opzichte van het gemiddelde.
- De grafiek loopt van min oneindig naar plus oneindig.
- Het gemiddelde, de mediaan en de modus van de verdeling zijn gelijk aan elkaar. De mediaan is het middelste getal in de waarnemingen als je de getallen op volgorde zet. De modus is de waarneming die het vaakst voorkomt.
- De mate van spreiding t.o.v. van het gemiddelde wordt weergegeven met σ.
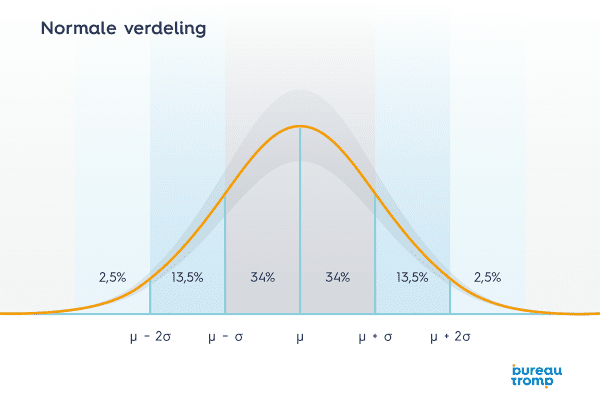
- De oppervlakte onder de grafiek hangt af van het aantal sigma t.o.v. het gemiddelde. Hierdoor kan je bijvoorbeeld stellen dat ongeveer 68% van de waargenomen waardes minder dan σ van μ afliggen. Onderstaande afbeelding verduidelijkt dit.
Six Sigma
De term Six Sigma stamt af van de normale verdeling. Het betekent dat idealiter 99,99966% van de producten (6σ aan beide zijden van het gemiddelde) binnen de gestelde marges presteert. Als we bij de appels stellen dat een zak minimaal 0,99 kg mag wegen en maximaal 1,01 kg, dan zou dat in 99,99966% van alle zakken appels het geval moeten zijn als we de 6σ-norm hanteren. Concreet betekent dit dat er maar 3,4 zakken per miljoen minder dan 0,99kg of meer dan 1,01 wegen.
In het geval van een zak appels is het waarschijnlijk niet nodig om zulke strakke marges te hanteren, maar wanneer je echter denkt aan de beschikbaarheid van internet of elektriciteit is er een zeer grote beschikbaarheid gewenst. In het geval van mogelijk levensbedreigende situaties, bijvoorbeeld wanneer je werkt met nucleaire stoffen, kan de norm van 6σ bijvoorbeeld niet voldoende zijn.
Niet normaal verdeelde data
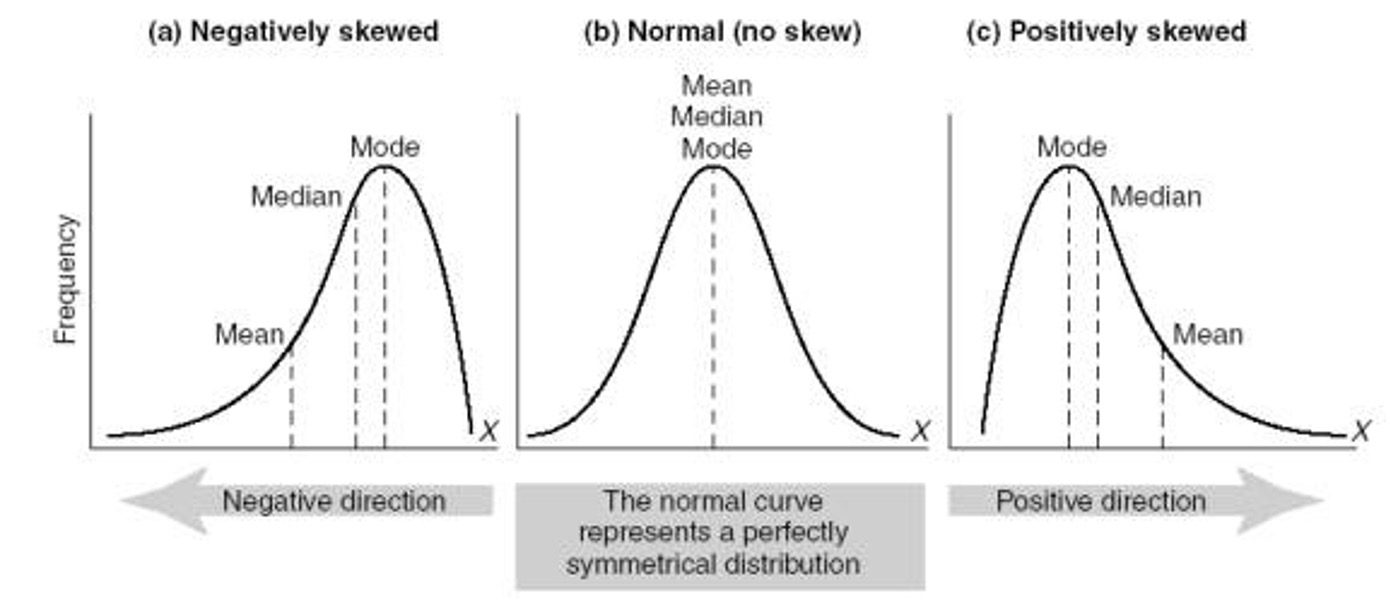
In de praktijk is data niet altijd normaal verdeeld. Denk bijvoorbeeld aan het scoringspercentage op een toets. De meest voorkomende score (modus) zal zo rond de 7,5 liggen met enkele uitschieters omhoog. Door relatief meer onvoldoendes zal de verdeling van de scores scheef zijn, zie de grafiek linksonder.
Dit heeft als effect dat de mediaan, het gemiddelde en de modus op een verschillende plek liggen, in tegenstelling tot een normale verdeling waar ze ongeveer gelijk aan elkaar zijn.
Maar waarom is dit nu eigenlijk een probleem?
Zonder helemaal in de technische kant te duiken van de statistiek, het volgende:
Bij een normale verdeling gebruik je bijvoorbeeld een t-test om hypothesen te testen. Deze t-test vergelijkt datasets op basis van gemiddelden. Aangezien de modus en mediaan ongeveer gelijk zijn, is dit de geijkte methode. Het gemiddelde geeft als centrummaat namelijk een goede indicatie van de resultaten van je steekproef.
Als het gemiddelde echter sterk afwijkt van de modus en mediaan (zie de scheve verdelingen), dan zegt het gemiddelde niet zoveel meer over de steekproef. De extreme waarden (de grotere hoeveelheid onvoldoendes ten opzichte van de hele hoge cijfers) brengen het gemiddelde van de groep ver omlaag, terwijl toch heel veel leerlingen een goed cijfer gescoord hebben.
Vergelijken van gemiddelden gaat dan niet op, omdat ze te weinig zeggen over de daadwerkelijke prestaties.
En nu?
Geen nood! Ook hiervoor zijn statistische tests ontworpen. Deze behandelen we niet tijdens de Lean Six Sigma Green Belt, maar wij wel bij Lean Six Sigma Black Belt.
Als we bovenstaand voorbeeld toepassen en we willen twee groepen leerlingen met elkaar vergelijken, kunnen we kiezen uit onder andere de Mood’s Median en Kruskall-Wallis testen. Deze twee testen vergelijken niet de gemiddelden van de groepen met elkaar, maar de medianen. Als je de grafieken bekijkt, zie je dat de medianen meer zeggen op de prestaties van de groep(en) en zijn de uitkomsten van je hypothesetesten dus een stuk betrouwbaarder.
Wil je meer weten over hypothese testen voor niet-normaal verdeel data? Schrijf je dan in voor een Lean Six Sigma Green to Black of Lean Six Sigma Black training.
Volg ons op LinkedIn (we delen onze artikelen met je)